Confirmatory Factor Analyses
lavaan package (Rosseel et al., 2023).
Revealjs Presentation
If you want to see the presentation in full screen go to Other Formats on the right. The presentation can be downloaded here.
Preface: Software
- The following packages are used:
- Install packages when not already installed:
Preface: Data
To demonstrate, we use the first measurement time point of a simulated data set. The data simulation is described in the Example Data section. Alternatively, you can download the wideLSdat.RDS file here.
wideLSdat <- readRDS("../example-data/wideLSdat.RDS")Confirmatory Factor Analysis (CFA): Overview
- Introduction & Purposes of CFA
- Parameters & graphical visualization
- Estimation of parameters
- Model identification
- Model evaluation
- Implementation in the R package lavaan (Rosseel et al., 2023)
CFA: Introduction
Confirmatory factor analysis” (CFA) is a type of structural equation modeling that deals specifically with measurement models, that is, the relationships between observed measures or “indicators” (e.g., items, test scores, behavioral observation ratings) and latent variables or “factors. (Brown & Moore, 2012, p. 361)
Goal: to establish the number and nature of factors (i.e., latent variables) that account for the variation and covariation among a set of indicators
- the indicators (i.e., observed measures) are intercorrelated because they share a common cause (or with other words: are influenced by the same underlying construct)
Purposes of CFA
Psychometric evaluation (e.g., Reliability; for scale reliability see here)
Detection of method effects (e.g., covariation among indicators, after the latent variable was partialed out)
Construct validation (e.g., convergent and discriminant validity); see also multi-trait-multi-method approaches (Campbell & Fiske, 1959)
Evaluation of measurement invariance (see here)
Scale development
CFA parameters & graphical visualization
- Variance of the latent variable: \(\Psi\)
- Intercepts: \(\nu\)
- Factor loadings: \(\lambda\)
- Error variances: \(\theta\)
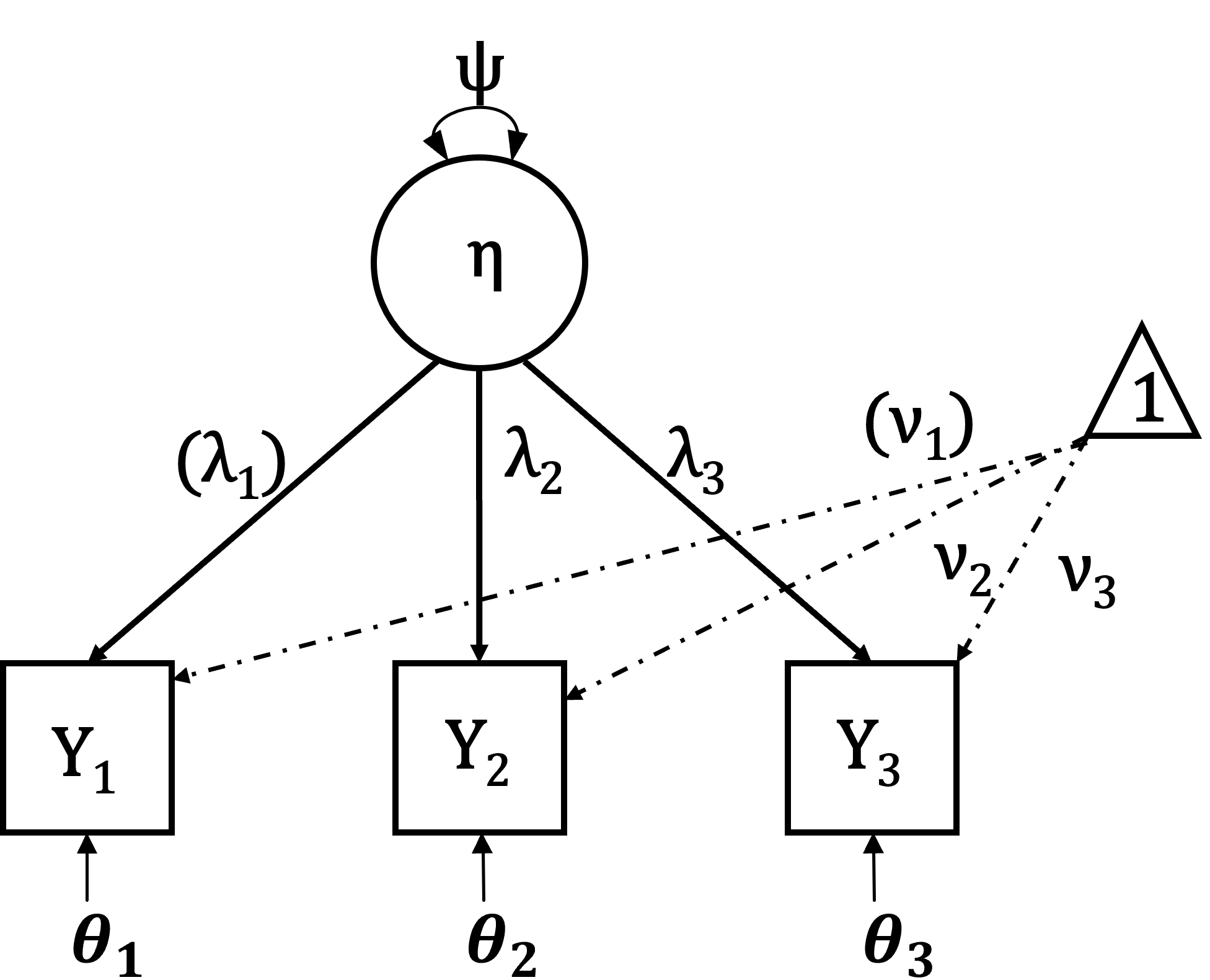
\[Y_i = \nu_i + \lambda_i\eta + \theta_i\]
Scale Reliability
- There is some debate about Cronbach’s Alpha Reliability Coefficient (Revelle & Zinbarg, 2009; Sijtsma, 2009)
Even though the pages of Psychometrika have been filled over the years with critiques and cautions about coefficient α and have seen elegant solutions for more appropriate estimates, few of these suggested coefficient are used.” (p.2)
- An alternative: Scale reliability
- […] “reliability“ as the ratio of true variance to observed variance […]” (Raykov & Marcoulides, 2015)
- Scale reliability: \(\rho = \frac{(\lambda_1+\dots+\lambda_k)^2}{(\lambda_1+\dots+\lambda_k)^2+\theta_1+\dots+\theta_k}\)
Estimation of (CFA-) Model Parameters
Model parameters are estimated on the basis of the empirical variances, covariances, and means
This is done by minimizing the discrepancy between a sample variance-covariance matrix \(S\) and a model-implied variance-covariance matrix \(\Sigma(\theta)\)
Fit function for ML (without means): \[F_{ML}=log|\Sigma(\theta)|+tr(S\Sigma^{-1}(\theta))-log|S|-p\]
- \(\theta\) = Model parameters
- \(p\) = number of parameters of observed variables
- \(tr\) = trace (spur)
Model identification I
Going from the known to the unknown (Kenny & Milan, 2012)
Known information: number of elements in the variance-covariance matrix and the mean vector
- In general with \(k\) measured variables, there are…
- k(k+1)/2 knowns (without meanstructure)
- k(k+3)/2 knowns (with meanstructure)
- In general with \(k\) measured variables, there are…
Unknown information: all parameters that need to be estimated
Correspondence of known and unknown information determines whether a model is
- underidentified
- just-identified
- overidentified
Model identification II
- Underidentified
- \(10 = 2x + y\)
- One piece of information; no unique solution (i.e., infinite solutions) for x and y
- just-identified (also referred as a saturated model)
- \(10 = 2x + y2 = x – y\)
- Two pieces of knowns; number of unknowns and knowns is equal
- Overidentified
- \(10 = 2x +y2 = x – y5 = x + 2y\)
- More known than unknown information
Goal of model testing: Overidentification (i.e., Falsifiability; degree of wrongness → Fit indices)
Model identification III
- Common SEM (!) situation
- constructs have multiple indicators,
- most indicators load only on one construct (i.e., “simple structure”),
- each indicator has the same possible response scale (i.e., range)
- Little et al. (2006) describe 3 methods
- Reference-Group Method: fixing the latent mean and the latent variance
- Marker-Variable Method: fixing intercept to zero and loading of one indicator to 1
- Effects-Coding Method: indicator intercepts sum to 0 the set of loadings sum to average 1
Model identification IV
Effects-Coding Method: indicator intercepts sum to 0 the set of loadings sum to average 1
loadings: \[\sum_{k=1}^{K} \lambda_{k} = K\]
intercepts: \[\sum_{k=1}^{K} \tau_{k} = 0\]
'
# a measurement model with 3 items
...
# constraints
lam1 == 3-lam2-lam3
nu1 == 0-nu2-nu3
'Model identification V
This method uses the effects constraints to provide an optimal balance across the possible indicators to establish the scale for the estimated parameters, where the average intercept is zero, but no individual manifest intercept is fixed to be zero. Similarly, the loading parameters are estimated as an optimal balance around 1.0, but no individual loading is necessarily constrained to be 1.0. This method results in estimates of the latent variances that are the average of the indicators’ variances accounted for by the construct, and the latent means are estimated as optimally weighted averages of the set of indicator means for a given construct. In other words, the estimated latent variances and latent means reflect the observed metric of the indictors, optimally weighted by the degree to which each indicator represents the underlying latent construct. (Little et al., 2006, p. 63)
Model evaluation
Common fit indices (Hu & Bentler, 1998, 1999) are …
\(\chi^2\) (Chi-square test statistic; cutoff: p < .05)
CFI (Comparative Fit Index; cutoff: > .95)
TLI (Tucker-Lewis Index; cutoff: > .95)
RMSEA (Root Mean Square Error of Approximation; cutoff: < .06)
SRMR (Standardized Root Mean Square Residual; cutoff: < .08)
Sometimes: AIC (Akaike Information Criterion) & BIC (Bayesian Information Criterion); no cutoffs
for a critique see McNeish & Wolf (2021)
Lavaan & Mplus syntax overview
| Formula type | Lavaan Operator | Mplus statement | Mnemonic |
|---|---|---|---|
| latent variable definition | =~ |
by |
is measured by |
| regression | ~ |
on |
is regressed on |
| (residual) (co)variance | ~~ |
with |
is correlated with |
| intercept | ~ 1 |
[ ] |
intercept |
| – | := |
= |
define functions |
| – | == |
== |
constraints |
CFA: lavaan implementation I
1CfaMod <- '
2eta1 =~ lam1*Y11 + lam2*Y21 + lam3*Y31
3Y11 ~ nu1*1
Y21 ~ nu2*1
Y31 ~ nu3*1
4Y11 ~~ theta1*Y11
Y21 ~~ theta2*Y21
Y31 ~~ theta3*Y31
5eta1 ~ 0*1
6eta1 ~~ 1*eta1 #psi
7rel := (lam1+lam2+lam3)^2 /
( (lam1+lam2+lam3)^2 +
theta1+theta2+theta3 )
'- 1
-
Use a string (i.e.,
' ') to specify the model; provide a recognizable and meanigful name (here:CfaMod) - 2
-
Specifiy the measurement model using the is measured by operator:
=~ - 3
-
(Optional) Specify the intercept of the item indicators using the intercept operatior:
~ 1 - 4
-
(Optional) Specify the residual variances of the item indicators using the is correlated with operator:
~~ - 5
-
(Optional) Specify the latent mean of the latent variable using the intercept operator:
~ 1 - 6
-
(Optional) Specify the variance of the latent variable using the is correlated with operator:
~~ - 7
- (Optional) Use the model constraint option, to calculate the scale reliability (Raykov & Marcoulides, 2015)
CFA: lavaan implementation II
- 1
-
To fit the model, you may want to use the
sem(orcfa) function - 2
-
In the
modelargument, you need to provide the specified model as a string (here:CfaMod). - 3
-
The dataset is provided in the
dataargument. - 4
-
Choose an estimator (default for continuous variable is
ML); in realworld scenarios you may want to choose a robust variant (e.g.,MLR). - 5
-
To fix the variance of the latent variabe to 1, we set the
std.lvargument toTRUE.
CFA: lavaan implementation III-I
- 1
-
To retrieve the results via the
summaryfunction (display only), you need to provide the object of the fitted model (here:fitCfaMod) - 2
-
The
fitargument: Whether the typical fit indices should be printed.
- 3
-
The
standardizedargument: Whether standardized solutions should be printed. - 4
-
The
rsqargument: Whether \(R^2\) should be printed.
The results are printed on the next slide.
CFA: lavaan implementation III-II
lavaan 0.6.15 ended normally after 17 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 9
Number of observations 1000
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Model Test Baseline Model:
Test statistic 157.517
Degrees of freedom 3
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.000
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -4604.807
Loglikelihood unrestricted model (H1) -4604.807
Akaike (AIC) 9227.615
Bayesian (BIC) 9271.785
Sample-size adjusted Bayesian (SABIC) 9243.200
Root Mean Square Error of Approximation:
RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: RMSEA <= 0.050 NA
P-value H_0: RMSEA >= 0.080 NA
Standardized Root Mean Square Residual:
SRMR 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta1 =~
Y11 (lam1) 0.563 0.059 9.460 0.000 0.563 0.488
Y21 (lam2) 0.576 0.061 9.500 0.000 0.576 0.494
Y31 (lam3) 0.558 0.059 9.470 0.000 0.558 0.490
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Y11 (nu1) -0.048 0.036 -1.324 0.185 -0.048 -0.042
.Y21 (nu2) -0.017 0.037 -0.461 0.644 -0.017 -0.015
.Y31 (nu3) -0.011 0.036 -0.297 0.766 -0.011 -0.009
eta1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Y11 (tht1) 1.012 0.071 14.246 0.000 1.012 0.762
.Y21 (tht2) 1.029 0.073 13.995 0.000 1.029 0.756
.Y31 (tht3) 0.988 0.070 14.183 0.000 0.988 0.760
eta1 1.000 1.000 1.000
R-Square:
Estimate
Y11 0.238
Y21 0.244
Y31 0.240
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
rel 0.487 0.028 17.345 0.000 0.487 0.487CFA: lavaan implementation IV
There are other ways to inspect or extract the results of the fitted model object
- Fit indices:
fitMeasuresfunction - Parameter:
parameterEstimatesfunction - Inspect/extraction function:
lavInspectlavInspect(object, what = "coef")lavInspect(object, what = "fit")lavInspect(object, what = "sampstat")lavInspect(object, what = "implied")- …
CFA: lavaan implementation: parameterEstimates
The parameterEstimates is designed to extract the estimated parameters of the model.
cfaParm <- parameterEstimates(fitCfaMod,
se = TRUE,
zstat = TRUE,
pvalue = TRUE,
ci = TRUE,
standardized = FALSE,
rsquare = TRUE)
cfaParm[cfaParm$label == "rel","rhs"] <- "" # just cosmetic
cfaParm lhs op rhs label est se z pvalue ci.lower ci.upper
1 eta1 =~ Y11 lam1 0.563 0.059 9.460 0.000 0.446 0.679
2 eta1 =~ Y21 lam2 0.576 0.061 9.500 0.000 0.457 0.694
3 eta1 =~ Y31 lam3 0.558 0.059 9.470 0.000 0.442 0.673
4 Y11 ~1 nu1 -0.048 0.036 -1.324 0.185 -0.120 0.023
5 Y21 ~1 nu2 -0.017 0.037 -0.461 0.644 -0.089 0.055
6 Y31 ~1 nu3 -0.011 0.036 -0.297 0.766 -0.081 0.060
7 Y11 ~~ Y11 theta1 1.012 0.071 14.246 0.000 0.873 1.152
8 Y21 ~~ Y21 theta2 1.029 0.073 13.995 0.000 0.884 1.173
9 Y31 ~~ Y31 theta3 0.988 0.070 14.183 0.000 0.851 1.124
10 eta1 ~1 0.000 0.000 NA NA 0.000 0.000
11 eta1 ~~ eta1 1.000 0.000 NA NA 1.000 1.000
12 rel := rel 0.487 0.028 17.345 0.000 0.432 0.542
13 Y11 r2 Y11 0.238 NA NA NA NA NA
14 Y21 r2 Y21 0.244 NA NA NA NA NA
15 Y31 r2 Y31 0.240 NA NA NA NA NACFA: lavaan implementation V: Fit indices
The fitMeasures is designed to extract the fit indices of the model.
Make a CFA Table
cfaResults <- cfaParm |>
subset(select = c("label", "est", "se", "pvalue")) |>
subset(subset = grepl("lam", label) |
grepl("rel", label)) |>
within(label <- c(paste0("\\lambda_", 1:3),
"Rel.")) |>
within(pvalue <- sprintf("%.3f", pvalue)) |>
print() label est se pvalue
1 \\lambda_1 0.563 0.059 0.000
2 \\lambda_2 0.576 0.061 0.000
3 \\lambda_3 0.558 0.059 0.000
12 Rel. 0.487 0.028 0.000cfaFN <- paste0(c("CFI = ", "TLI = ", "RMSEA = ", "SRMR = "),
sprintf("%.3f",cfaFit[c("cfi", "tli", "rmsea", "srmr")]),
collapse = ", ")
cfaFN[1] "CFI = 1.000, TLI = 1.000, RMSEA = 0.000, SRMR = 0.000"Print the CFA Table
cfaResults |>
flextable() |>
theme_apa() |>
set_header_labels(
"label" = "Parameter",
"est" = "Estimate",
"se" = "SE",
"pvalue" = "p") |>
compose(j = "label", i = 1:3,
value = as_paragraph((as_equation(label)))) |>
add_footer_lines(
as_paragraph(as_i("Note. "),
cfaFN)
) |>
align(align = "left", part = "footer")Parameter | Estimate | SE | p |
|---|---|---|---|
NA | 0.56 | 0.06 | 0.000 |
NA | 0.58 | 0.06 | 0.000 |
NA | 0.56 | 0.06 | 0.000 |
Rel. | 0.49 | 0.03 | 0.000 |
Note. CFI = 1.000, TLI = 1.000, RMSEA = 0.000, SRMR = 0.000 | |||
Code
install.packages("equatags")